Planar Carbon Lattices

B2 - Structural, electronic, and vibronic topology in PCLs

Principal investigator: Prof. Dr. Thomas Heine, TU Dresden, [webpage]
Doctoral researcher Diyan Unmu Dzujah

It has been demonstrated that the emergence of topologically non-trivial electronic structure depends on the edge structure in one-dimensional graphene nanoribbons (1D GNRs)[1,2] and on the 2D lattice type for 2D polymers (2DPs).[3] These new forms of quantum matter offer a significantly larger space of lattice topologies compared to their inorganic competitors. As known from graphene, due to their composition of light-weight atoms, spin-orbit coupling (SOC) is weak and typically yields only tiny band gaps that prohibit application beyond cryogenic temperature. However, in PCLs, a sizable band gap can be opened by quantum confinement (size control), structural elements as coves and chirality (edge control), and by chemical perturbation.[3] New synthesis approaches have led to PCLs of high structural quality for which topological properties such as Dirac points and flat bands. The possibility to tailor the electronic topological structure of graphene by patterning remains unexplored, and even for GNRs and 2DPs only a small portion of the rich chemical space that can yield topologically non-trivial states have been investigated. For similarly interesting topological vibrational states very little work has been reported to date. We propose to computationally screen new topological 2DPs, bridge top-down and bottom-up synthesis by exploring GNRs and associated patterned graphene with the same structural topology for their electronic and, at a later stage, vibronic topological properties.

© Thomas Heine

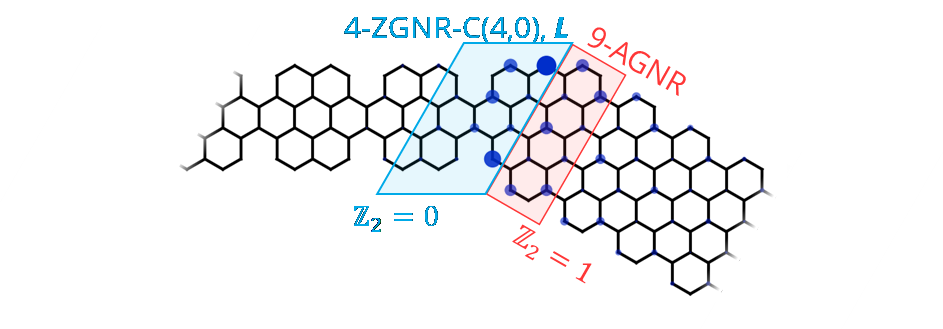
Figure: Topological junction state at the intersection of a cove-edged zigzag and an armchair graphene nanoribbon.[2]

A graph-topological scheme suggesting construction routes of specific GNRs from programmed monomers will be developed. The structural, electronic, vibronic and topological properties will be predicted employing a range from first-principles methods (RPA, GW, DFT) towards TB. Topological indexes (Chern number and Z_2 invariant) will be determined by Berry phase integration and by the parity method.

Thesis topic: Topological GNRs and patterned graphene with large gap

We will explore the entire chemical space of GNRs and patterned graphene. The first one allows for chirality and for a rich cove structure, while the latter offers the introduction of superlattices on top of graphene’s electronic π-system. Both approaches allow for altering topological properties and introducing a band gap. We will closely collaborate with the groups of Feng (GNRs), Hirsch (patterned graphene) and Maultzsch (vibronic properties).